相関データと
サンプルサイズ設計
デルタ法のサンプルサイズ設計には気をつけて
statditto
2024-10-19
自己紹介
- X:@st4tditt0
- 社会人2年目
- R歴は4年くらい

今日話すこと
- 相関データのA/Bテスト
- デルタ法を用いた仮説検定
- デルタ法のサンプルサイズ設計
まとめ
- 相関データは適切な手法で対処すべき
- デルタ法を用いる際には、サンプルサイズ設計もデルタ法に適したものを選択すべき
- 相関を無視すると、意図せず誤った結論が導かれる恐れがある
話さないこと
- 細かい理論の話
- 気になる方は参考文献からどうぞ!
相関データのA/Bテスト
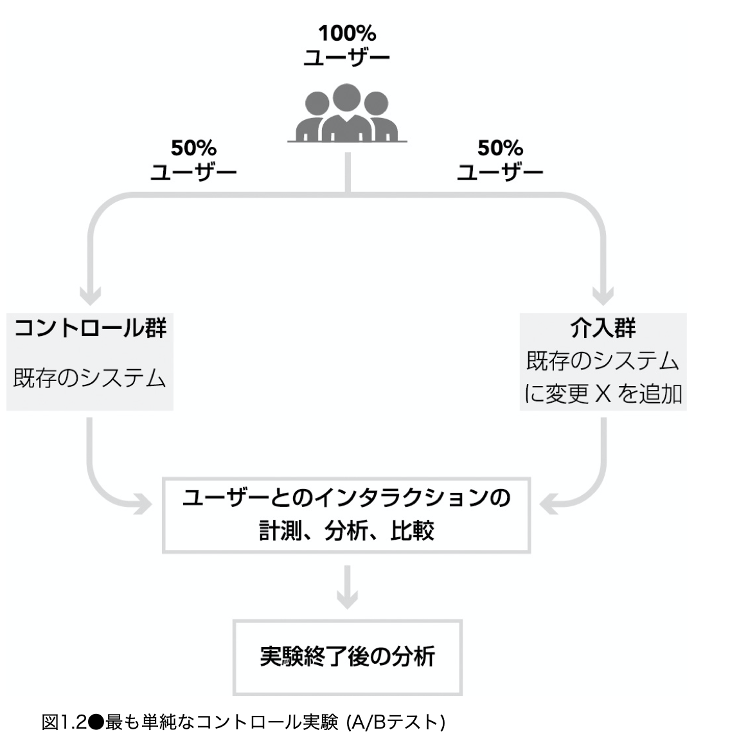
A/Bテスト
- 異なる実験群(Control, Treat)を比較し、その効果を測定する実験手法
- ユーザーを無作為に割り当てることが多い
- 次のA/Bテストを例に考える
- 概要:あるWebサイトのコンテンツを新しいものに入れ替える施策
- 指標:CTR(総click数/総impression数)
- 手法:母比率の差の検定

データ例
- dt:日付
- user_id:ユーザーid
- impressions:コンテンツのimpression数
- clicks:コンテンツのclick数
サンプルサイズ設計
- 有意水準0.05、検出力0.80の両側検定として設計
power.prop.test(p1 = 0.30, # C群のCTR(過去のデータから30%とわかっている)
p2 = 0.31, # T群のCTR(1%ptの効果量を仮定)
sig.level = 0.05, # 有意水準α(真に差がない時に誤って帰無仮説を棄却してしまう割合)
power = 0.8) # 検出力β(真に差がある時に正しく差を検出できる割合)
Two-sample comparison of proportions power calculation
n = 33274.15
p1 = 0.3
p2 = 0.31
sig.level = 0.05
power = 0.8
alternative = two.sided
NOTE: n is number in *each* group- 必要なimpression数は各群33275件
- 各群で必要なユーザー数を計算
- 過去のデータでは、1ユーザーあたりの平均impression数は353.5件らしい
- [必要impression数]/[平均impression数]=33275/353.5=95人
A/Aテスト
- 同質なC群とT群を用意して、A/Aテストを行ってみる2
- 同質な2群の差を検定しているため有意差は出ないはず!
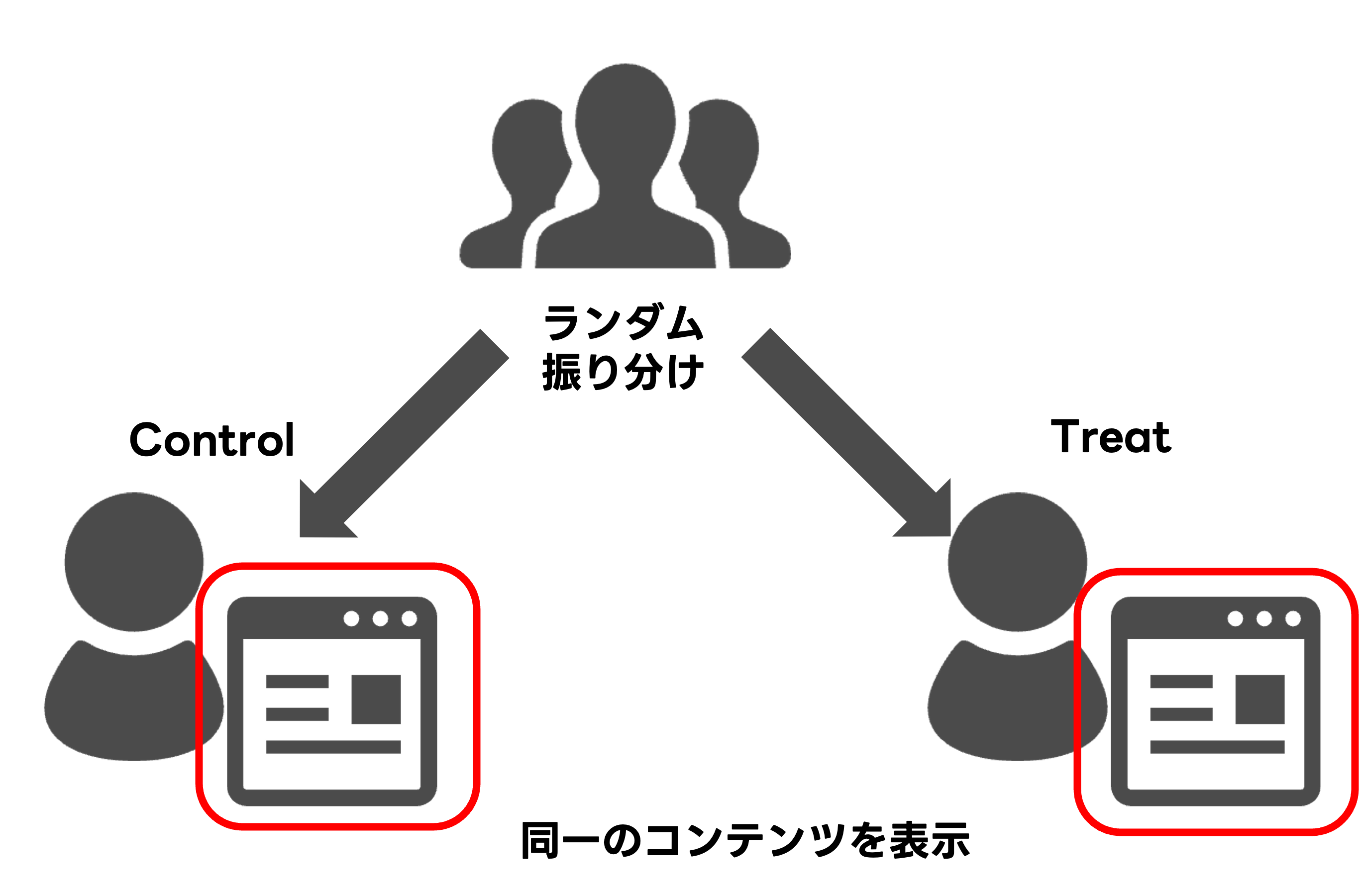
A/Aテストのイメージ
A/Aテストをやってみる
control <- get_control_data(95) %>%
summarise(imp = sum(impressions),
click = sum(clicks))
treat <- get_control_data(95) %>%
summarise(imp = sum(impressions),
click = sum(clicks))
aa <- bind_rows(control,treat) %>%
mutate(group = c("C_1", "C_2")) %>%
select(group, imp, click) %>%
mutate(CTR = click/imp)| group | imp | click | CTR |
|---|---|---|---|
| C_1 | 34606 | 10370 | 0.30 |
| C_2 | 35097 | 9952 | 0.28 |
2-sample test for equality of proportions with continuity correction
data: aa$click out of aa$imp
X-squared = 21.795, df = 1, p-value = 3.034e-06
alternative hypothesis: two.sided
95 percent confidence interval:
0.009325615 0.022878424
sample estimates:
prop 1 prop 2
0.299659 0.283557 - 有意差が出た
- \(\alpha=0.05\)の設計なので偶然5%を引いてしまったか……?
たくさんやってみる
- 何度もA/Aテストをやってみる
- 正しくテスト設計ができていれば、p値は一様分布になる3
simulate_test <- function(i) {
control <- get_control_data(95) %>%
summarise(imp = sum(impressions),
click = sum(clicks))
treat <- get_control_data(95) %>%
summarise(imp = sum(impressions),
click = sum(clicks))
tmp <- bind_rows(control, treat)
tmp <- prop.test(n = tmp$imp, x = tmp$click)
tmp$p.value
}
p_values <- future_map_dbl(1:1000,
simulate_test,
.options = furrr_options(seed = 123)
,.progress = TRUE)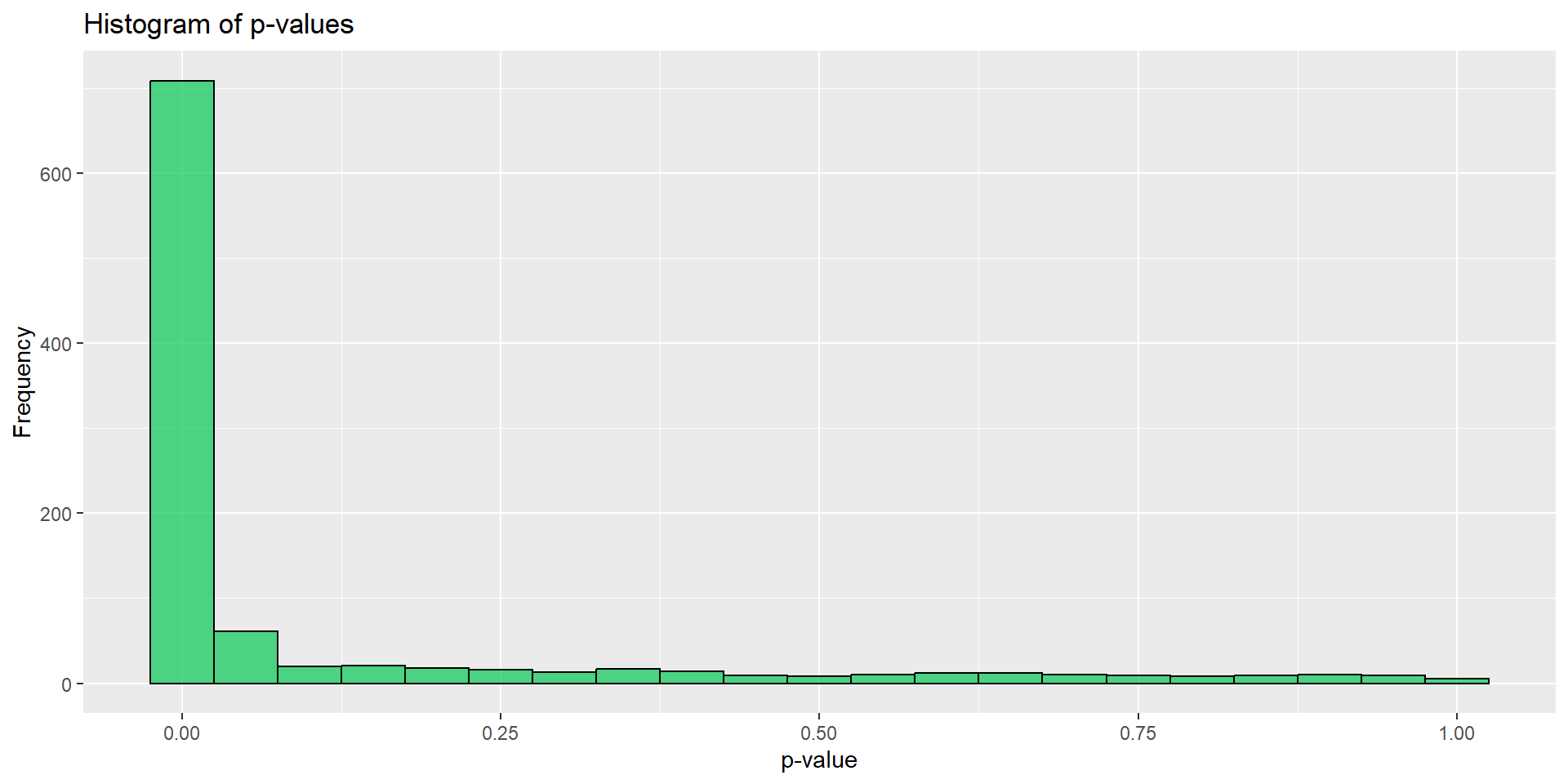
どうして……?
- 今回の例ではユーザー単位でランダム化を行った
- 分析対象の指標はimpression単位
- ランダム化単位と分析単位が異なる時は注意が必要
- 今回利用した検定は標本にi.i.d.を仮定している
- 実際は同一ユーザーの試行は相関がある(ことがある)
→仮定が満たされない状況下で検定してしまった
手法が必要とする仮定を満たさない状況下では誤った結論を導く可能性がある
相関データへの対処
相関データに対する議論
数式で書き直す(苦しい)
- ユーザーと観測データ
- ユーザー数:\(k\)
- 各ユーザー \(i\) のimpression数:\(N_i\)
- clickの有無:\(X_{ij}\)
(\(i = 1, \ldots, k;j = 1, \ldots, N_i\))
- 指標の再定義
- 平均値: \(\bar{X} = \frac{\sum_{i,j} X_{ij}}{\sum_i N_i} = \frac{\sum_i S_i / k}{\sum_i N_i / k} = \frac{\bar{S}}{\bar{N}}\)
- ここで、\(S_i = \sum_j X_{ij}\)
- 各パラメータ
- click数の期待値:\(\mu_S = \mathbb{E}(S_i)\)
- impression数の期待値:\(\mu_N = \mathbb{E}(N_i)\)
- click数の分散:\(\sigma_S^2 = \text{Var}(S_i)\)
- impression数の分散:\(\sigma_N^2 = \text{Var}(N_i)\)
- click数とimpression数の共分散:\(\sigma_{SN} = \text{Cov}(S_i, N_i)\)
デルタ法
- 指標に注目:\(\bar{X} = \frac{\sum_{i,j} X_{ij}}{\sum_i N_i} = \frac{\sum_i S_i / k}{\sum_i N_i / k} = \frac{\bar{S}}{\bar{N}}\)
- \(\bar{S}, \bar{N}\)は極限では多変量正規分布に従うとみなせる
- それらの比\(\bar{X}\)が正規分布に従うことが知られている(デルタ法)
- デルタ法で推定された分散
- \(\text{Var}\left(\frac{\bar{S}}{\bar{N}}\right) \approx \frac{1}{k\mu_N^2} \left( \sigma_S^2 - 2 \frac{\mu_S}{\mu_N} \sigma_{SN} + \frac{\mu_S^2}{\mu_N^2} \sigma_N^2 \right)\)
- 導出にはテーラー展開を用いるが、ここでは省略(こちらのブログが丁寧9)
- 推定した分散を用いて検定
Rによる実装
var_delta <- function(x, y){
mean_x <- mean(x)
mean_y <- mean(y)
var_x <- var(x)
var_y <- var(y)
cov_xy <- cov(x, y)
result <- (var_x / mean_x**2 + var_y / mean_y**2 - 2 * cov_xy /
(mean_x * mean_y)) * (mean_x * mean_x) / (mean_y * mean_y * length(x))
return(result)
}
delta_test <- function(mean_x, mean_y, var_x, var_y){
diff = mean_y - mean_x
var = var_x + var_y
z = diff / sqrt(var)
p_val <- 2 * pnorm(abs(z), lower.tail = FALSE)
result <- data.frame(difference = diff, p_value = p_val)
return(result)
}Re:たくさんやってみる(A/A)
simulate_test <- function(i) {
control <- get_control_data(95) %>%
summarise(imp = sum(impressions),
click = sum(clicks),
.by = user_id)
treat <- get_control_data(95) %>%
summarise(imp = sum(impressions),
click = sum(clicks),
.by = user_id)
mean_c <- sum(control$click)/sum(control$imp)
mean_t <- sum(treat$click)/sum(treat$imp)
var_c <- var_delta(control$click, control$imp)
var_t <- var_delta(treat$click, treat$imp)
tmp <- delta_test(mean_c, mean_t, var_c, var_t)
tmp$p_value
}
p_values_aa <- future_map_dbl(1:1000,
simulate_test,
.options = furrr_options(seed = 123)
,.progress = TRUE)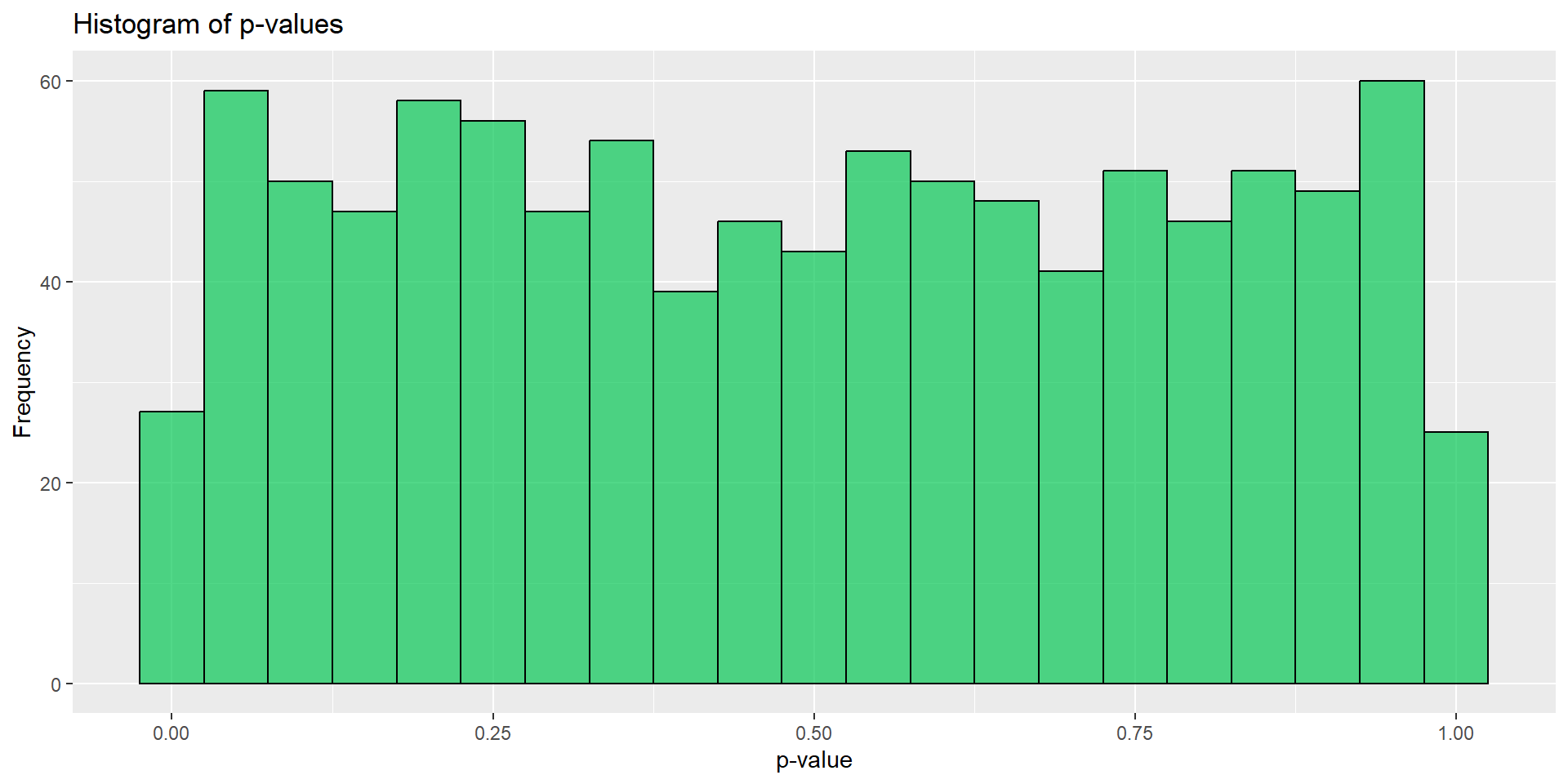
- 概ね一様分布していそうに見える
- 少なくともさっきよりはマシ
Re:たくさんやってみる(A/B)
simulate_test <- function(i) {
control <- get_control_data(95) %>%
summarise(imp = sum(impressions),
click = sum(clicks),
.by = user_id)
treat <- get_treat_data(95) %>%
summarise(imp = sum(impressions),
click = sum(clicks),
.by = user_id)
mean_c <- sum(control$click)/sum(control$imp)
mean_t <- sum(treat$click)/sum(treat$imp)
var_c <- var_delta(control$click, control$imp)
var_t <- var_delta(treat$click, treat$imp)
tmp <- delta_test(mean_c, mean_t, var_c, var_t)
tmp$p_value
}
p_values_ab <- future_map_dbl(1:1000,
simulate_test,
.options = furrr_options(seed = 123)
,.progress = TRUE)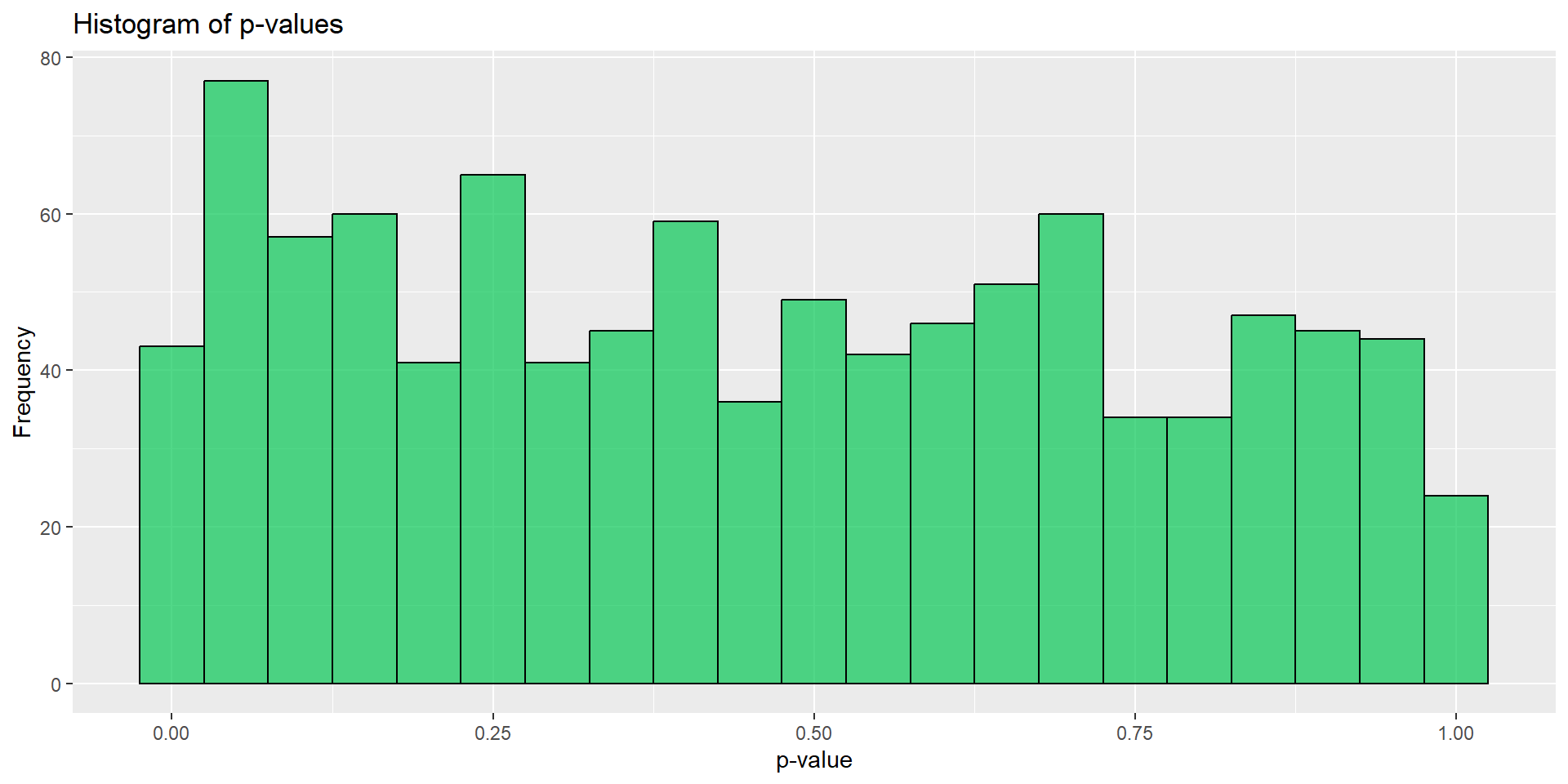
- \(p<0.05\)となる試行はたったの8.2%しかない
- 検出力80%で設計しているのにどうしてこんなことに
デルタ法のサンプルサイズ設計
何がダメだったか
- 通常のA/Bテストで設計したサンプルサイズでは検出力が大幅に不足してしまう
- 過小評価された分散を設計に用いているから
- デルタ法で推定した分散をサンプルサイズ設計でも利用すべき10
- 通常のサンプルサイズ設計の式:\(n = 2 \sigma^2 \cdot (z_{1- \alpha /2} + z_{1-\beta}) /\delta^{2}\)
- \(\text{Var}(\bar{X}) = \sigma^2/n\)であることを利用して、代入し整理する
\[ \begin{aligned} k &= 2h・(z_{1-\frac{\alpha}{2}} + z_{1-\beta}) / \delta^{2}, \\ ただし,h &= \frac{1}{\mu^2_{N}}( \sigma^{2}_{S} - 2\frac{\mu_{S}}{\mu_{N}}\sigma_{SN} + \frac{\mu^{2}_{S}}{\mu^{2}_{N}}\sigma^{2}_{N} ) \end{aligned} \]
Rによる実装
- この関数でサンプルサイズ設計をやり直すと3427人必要だとわかる
- 通常の設計で求められた95人の36.4倍!
- 実は全くサンプルサイズが足りていなかった
Re:Re:今度こそ
simulate_test <- function(i) {
control <- get_control_data(3427) %>%
summarise(imp = sum(impressions),
click = sum(clicks),
.by = user_id)
treat <- get_treat_data(3427) %>%
summarise(imp = sum(impressions),
click = sum(clicks),
.by = user_id)
mean_c <- sum(control$click)/sum(control$imp)
mean_t <- sum(treat$click)/sum(treat$imp)
var_c <- var_delta(control$click, control$imp)
var_t <- var_delta(treat$click, treat$imp)
tmp <- delta_test(mean_c, mean_t, var_c, var_t)
tmp$p_value
}
p_values_ok <- future_map_dbl(1:200,
simulate_test,
.options = furrr_options(seed = 123)
,.progress = TRUE)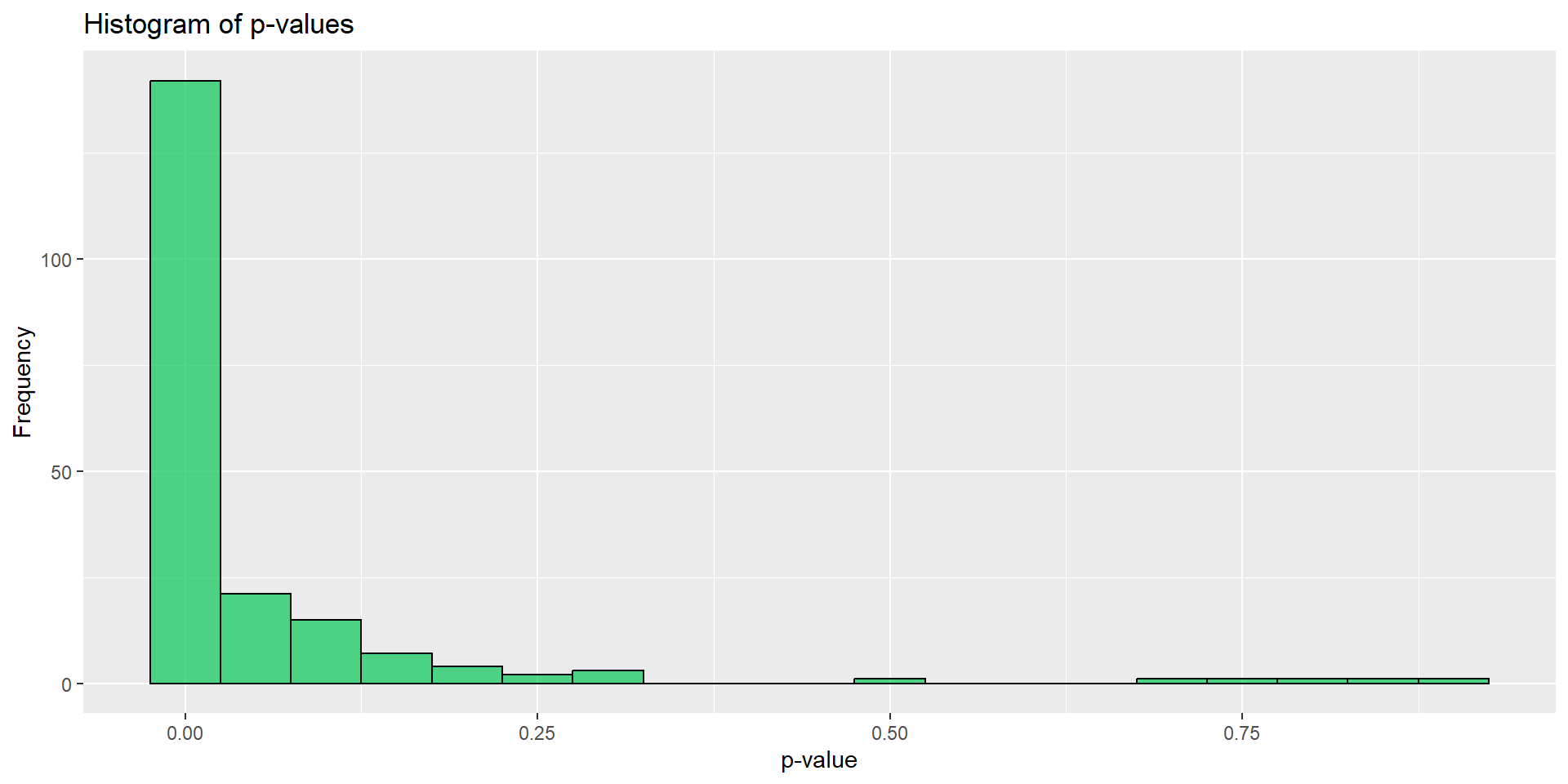
- \(p<0.05\)となる試行は78%
- やったね!
実用上の注意点(特にWebの世界)
- サンプルサイズ設計の式をもう一度
- \(h = \frac{1}{\mu^2_{N}}( \sigma^{2}_{S} - 2\frac{\mu_{S}}{\mu_{N}}\sigma_{SN} + \frac{\mu^{2}_{S}}{\mu^{2}_{N}}\sigma^{2}_{N})\)
- 実験期間の変更に応じて平均、分散、共分散も変化してしまう
- 実務的には次のフローで行うと良さそう
- 実験期間の候補を定める(e.g. 1 week or 2 week)
- 効果量の候補を定める(\(\delta=\{0.01, 0.05\}\))
- 実験期間ごとに平均、分散、共分散を求める
- \(h\)を計算(e.g. h_1week, h_2week)
- \(\delta,h\)の組み合わせごとにサンプルサイズを求める
- どの設定で実施するか考える
まとめ
デルタホウカンゼンニリカイシタ
- 相関データには気をつけろ!
- デルタ法は便利だけど正しく使わないと危ないぞ!
- A/Bテストを正しくやるのは難しい;;
- 手法が必要とする仮定を意識して利用したい
Enjoy!
データ生成過程
独立な試行ではあるが同一でない分布を仮定していた
- ユーザーID
- ユーザー数 \(k\) に対して、ユーザーIDは \(1, 2, \ldots, k\)
- 各ユーザーの真のCTR
- \(p_i \sim \text{Beta}(3.0, 7.0)\)
- impressionとclick
- 各日付に対して、impressionが発生するかどうかをサンプル \(\text{is\_impression}_i \sim \text{Bernoulli}(0.5)\)
- 発生した場合
- \(N_i \sim \text{Uniform}(1, 100)\)
- \(S_i \sim \text{Binomial}(\text{is\_impression}_i, p_i)\)
Reference
1.
Ron K, Diane T, Ya X. A/Bテスト実践ガイド. アスキードワンゴ; 2021.
2.
Kohavi R, Longbotham R, Sommerfield D, Henne RM. Controlled experiments on the web: Survey and practical guide. Data Min Knowl Discov. 2009;18(1):140-181. doi:10.1007/s10618-008-0114-1
3.
gota morishita. なぜAAテストにおけるp値は一様分布になるのか?. 2021. https://zenn.dev/morishita/articles/3c77d00b303c76
4.
Deng A, Knoblich U, Lu J. Applying the delta method in metric analytics: A practical guide with novel ideas. In: Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. KDD ’18. Association for Computing Machinery; 2018:233-242. doi:10.1145/3219819.3219919
5.
Taro T. 統計指標の信頼区間を評価する delta method とその応用(論文紹介). 2018. https://engineering.linecorp.com/ja/blog/delta-method
6.
中村. 検索エンジンのABテストで発生するユーザー内相関を突破する. 2021. https://www.m3tech.blog/entry/search-ab
7.
伊藤, 藤田. なぜあなたのA/Bテストはうまくいくのか?a/Bテストの分析で注意すること. 2021. https://developers.cyberagent.co.jp/blog/archives/33310/
8.
伊藤寛武, 金子雄祐. Pythonで学ぶ効果検証入門. オーム社; 2024.
9.
sz_dr. 確率変数の比の分布における平均と分散をデルタ法で求める. 2018. https://www.szdrblog.info/entry/2018/11/18/154952
10.
Zhou J, Lu J, Shallah A. All about sample-size calculations for a/b testing: Novel extensions & practical guide. In: Proceedings of the 32nd ACM International Conference on Information and Knowledge Management. CIKM ’23. Association for Computing Machinery; 2023:3574-3583. doi:10.1145/3583780.3614779